纤维的吸湿和导湿性能是直接影响织物穿着舒适性的重要因素。一类由合成纤维改性得到的吸湿排汗类功能纤维及其织物开发问世后迅速成为服用纤维市场上的热点。吸湿排汗纤维的主要改性方法有纤维细旦化、纤维异形化和化学表面处理等。

　　越来越多的学者致力于纤维集合体吸导湿行为的研究。然而，现阶段的研究多局限于对已有产品的测试分析，在数学模型的基础上，利用计算机模拟研究纤维集合体吸湿导湿性能还未见报道。本文将重点研究纤维细旦化对纤维集合体吸湿导湿性能的影响。

　　1纤维集合体吸湿导湿机制

　　合成纤维集合体的吸导湿行为主要是液体在纤维集合体中毛细孔隙的芯吸效应一。芯吸效应是指纤维集合体润湿之后，液体在界面张力的作用下沿着纤维集合体内毛细孔隙流动扩散的现象，它是纤维集合体具有吸导湿性能的主要原因。

　　1.1纤维集合体吸导湿途径

　　纤维织物的结构普遍遵循纤维、纱线、织物3层结构，若干根纤维集成纤维束形成纱线，若干纱线再经织造得到织物。这种多层次的结构使织物内形成几种不同性质的毛细孔隙，包括纱线内的毛细孔隙和纱线之间的毛细孔隙。这些毛细孔隙均有可能成为液体芯吸扩散的通道。而纱线内纤维与纤维之间的毛细孔隙是织物导湿的主要途径，即织物的导湿性能主要取决于纤维纱线（即纤维束）的导湿性能。

　　1.2纤维束垂直芯吸模型

　　明确了纤维集合体吸湿导湿的主要方式和途径后，本文将研究的重点聚集到纤维束内的芯吸过程。

　　Reed和Wilson为了研究液体在毛细空间中的扩散传输情况，提出一种简单的单毛细管垂直芯吸模型]，如图1所示。通过对毛细管内的液体进行受力分析可知，该段液体除了受到因液体界面张力产生的附加压力P之外，还受到与液体运动方向相反的液体自身重力Pc，液体黏滞力Pv，流体惯性力P1。

　　液体在毛细管内的芯吸流动是个动态的过程，假设液体流动时加速度为0，即流体惯性力P1，为0，此时对力学平衡方程式（2）积分求解可以得到液体芯吸流动的动力学方程：

　　由式（3）～（6）可见，毛细管芯吸性能参数h、Q、v等主要取决于液/气界面张力，固/液接触角θ，毛细管截面几何尺寸c、A，当纤维与液体固定时，.p、T、θ为定值，毛细管芯吸性能主要取决于毛细管截面几何尺寸。

　　在Reed&Wilson垂直芯吸模型的基础上，本文提出了纤维束垂直芯吸模型（modeloffiberbundle，简称MFB）。将一束纤维看作为若干根纤维平行排列，纤维之间相互接触，但不发生挤压形变。纤维与纤维之间形成若干平行排列毛细孔道，这些毛细孔道就是纤维束芯吸导湿的通道。类似Reed&Wilson模型，可以表征纤维束的最大芯吸高度：

　　芯吸高度、芯吸量、芯吸时间和芯吸速度等参数普遍用来表征纤维集合体的导湿性能。从这些导湿性能参数的表达式中可看出，在纤维材料与液体不变的情况下（即p、T、θ为定值），纤维束的导湿性能参数取决于纤维束内毛细管数量及其截面几何尺寸。如何获得纤维束内毛细管的数量以及几何尺寸成为评价纤维束导湿能力的关键。如图2所示，在纤维束轴向上取相距为f的两截面间的一段加以研究，利用无限分割原理，即当l趋向于无穷小时，纤维束段即等效为截面A或截面B。在截面A或B中可以直观地观察每根纤维在纤维束中的排列情况以及纤维束内毛细管生成情况。由于纤维束中纤维排列的随机无规性，纤维束可以看成无限多无差别的截面累积，所以应用MFB模型研究纤维束导湿性能的关键是纤维束截面图像的获得以及截面中毛细孔数量和几何尺寸的精确测量。

　　2纤维束截面的计算机模拟

　　为了获得纤维束内毛细孔数量及其几何尺寸，文献]通过假设纤维在纤维束中规则而紧密地排列，计算出纤维束截面中毛细孔隙的数量和尺寸，但这种理想的排列和实际情况下纤维无规随机的排列差异明显，结果参考意义不大。文献]通过拍摄纤维束截面照片，对照片进行图像分析来获得纤维束截面中毛细孔隙的数量和尺寸，这种方法同样存在缺陷。图像拍摄过程往往会使纤维束中纤维排列过于紧密，纤维往往会受压变形，而在图像分析时，模糊的纤维轮廓使毛细孔隙界定十分困难。

　　为了便捷高效并且尽可能准确地获得纤维束截面图像，并精确计算获得截面中毛细孔数量和几何尺寸，本文利用VisualC++编程软件开发了一套纤维束截面模拟软件，命名为SG（Shape.Generator）。通过该模拟软件实现纤维在纤维束中排列分布的仿真，获得纤维束截面的仿真图像，并通过图像处理精确计算出纤维束截面中毛细孔数量和几何尺寸。模拟所得的纤维束截面图中纤维完全随机排列，与实际纤维束中纤维排列情况十分接近，仿真度很高。

　　3模拟实验

　　在MFB模型的基础上，利用SG模拟软件模拟研究在相同的纱线尺寸下，单纤维线密度的变化对纱线内毛细孔隙的生成情况以及纱线的导湿性能所产生的影响。

　　3.1实验条件

　　实验以PTT纤维为例，模拟14种不同线密度的PTT纤维所组成纱线的芯吸性能。如表1所示，纱线截面直径一致，室温环境下纱线直径D为100um，纤维密度P为1.33×103。kg/m3，液/气表面张力T为7.2×10-3N/m，固/液接触角为60。，液体密度P为1×103kg/m3，液体黏度n为1×10-3Pa·s，重力加速度g取9.81m/s2。

　　3.1实验条件

　　实验以PTT纤维为例，模拟14种不同线密度的PTT纤维所组成纱线的芯吸性能。如表1所示，纱线截面直径一致，室温环境下纱线直径D为100um，纤维密度P为1.33×103。kg/m3，液/气表面张力T为7.2×10-3N/m，固/液接触角为60。，液体密度P为1×103kg/m3，液体黏度n为1×10-3Pa·s，重力加速度g取9.81m/s2。

　　由图4可见，随着纤维线密度值的降低，单纤维毛细孔生成能力并不是持续增加的，在0.36dtex左右达到峰值，此后随着纤维线密度值进一步减小，其单纤维毛细孔生成能力反而下降，并固定在一个特定值0.43左右。依此判断，当纤维过细时，纤维之间的孔隙因面积过小而堵塞，以至不能形成更多有效毛细孔。

　　3.2.2纤维束最大芯吸高度

　　最大芯吸高度指毛细孔在无限时间内芯吸爬升的最大高度。由图5可见，随着纤维线密度值的减小，纤维束内毛细孔的最大芯吸高度持续增加，并在0.36dtex时达到最大值，随着纤维进一步变细，其最大芯吸高度反而下降。

　　3.2.3纤维束最大芯吸量

　　最大芯吸量是指当芯吸达到最大高度时纤维束内的液体总量，它反映了纤维束对液体的承载能力。

　　由图6可见，纤维束的最大芯吸量随着纤维线密度值的减小而增大，并在纤维线密度为0.36dtex时达到最大值，此后随纤维进一步变细，最大芯吸量反而降低。这是因为纤维过细，纤维之间毛细孔容易阻塞而使纤维束孔隙率下降。

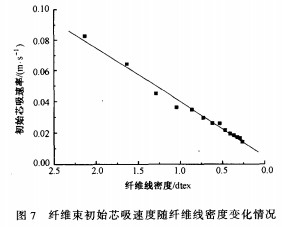
　　3.2.4纤维束初始芯吸速度

　　纤维束芯吸速度的快慢可以反映其导湿快干性能的好坏，特别是纤维束接触水分瞬间时的初始芯吸速度决定了织物能否迅速导湿快干。由式（9）（纤维束芯吸动力学方程）可知，纤维束的芯吸速度是逐渐趋缓的，在芯吸开始瞬间（t=0，x=0）趋向于无穷大。为了得到1个可以比较的芯吸速度值，将芯吸刚刚开始即芯吸高度达到0.1mm时的瞬间芯吸速度视为初始芯吸速度。由图7可见，随着纤维线密度值的减小，纤维束的初始芯吸速度呈线性下降趋势。可见细旦纤维虽然吸湿保水性能较好，但是导湿快干性能反而不如常规纤维。

　　4结论

　　纤维的线密度影响着纤维束内毛细孔的生成数量及其几何性质，从而影响纤维束的芯吸性能。综合上述模拟实验结果可知：相比常规PTT纤维，纤维细旦化有利于纤维束吸湿保水能力的提高，但并不是越细越好。当单纤维线密度为0.36dtex左右时，其纤维集合体的毛细孔生成能力最强，纤维集合体的最大芯吸高度、最大芯吸量均达到峰值，所以此时纤维集合体拥有最佳的吸湿保水能力，但是，纤维细旦化也使得纤维束的导湿快干性能下降。由此可见，一昧地纤维细旦化开发吸湿排汗类纤维是不可取的。

　　来源 王亚光，王华平，王朝生，张玉梅

该文章暂时没有评论！